| De la Gravitation Newtonnienne à la Relativité Générale d' Einstein |
Le texte de ce fichier provient en très grande partie de celui de Mr. Sébastien Charnoz publié dans Histoire du concept de gravitation |
|
|
E=mc2 |
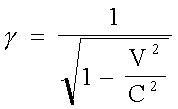 |
Albert Einstein Ses travaux touchent à de nombreux domaines de la physique : mécanique, relativité, effet photoélectrique (qui lui donnera un prix Nobel), mouvement brownien, physique statistique etc..
Le mouvement d'une particule doit être décrit dans un référentiel dit inertiel, c'est à dire un référentiel dans lequel une particule soumise à aucune force, continue son mouvement en ligne droite.
Au 19ème siècle la lumière était décrite comme une onde électromagnétique et on se demandait dans quel milieu se propage t'elle?Autrement dit, quel est le milieu qui transporte les rayons lumineux.
Dans un article écrit en 1878 dans l'Encyclopedia Britannica, Maxwell propose qu'un milieu très dilué, baignant l'univers dans son entier, et s'appelant Ether, soit le milieu physique qui supporte la propagation de la lumière. A l'Ether devait être rattaché un référentiel (3 axes d''espace et un de temps) inertiel et absolu. Maxwell proposa différentes expériences pour mesurer le déplacement de la Terre et de Jupiter dans cet Ether. Cette recherche était motivée également par un fait curieux dans les équations de l'électromagnétisme découvertes par Maxwell : les équations font toutes intervenir, une certaine grandeur appelée C, donnée comme étant la vitesse de la lumière. Se pose alors la question : la vitesse dans quel repère ? L'existence d'un référentiel absolu permettait de réécrire les équations de Maxwell dans ce repère, ce qui levait l'ambiguïté.
| C'est dans ce contexte que les deux physiciens expérimentateurs Michelson et Morley tentèrent de mesurer la vitesse de l'Ether par rapport à la Terre en 1887, en mesurant la vitesse de la lumière dans le sens de déplacement de la Terre autour du Soleil, puis dans le sens opposé. Le raisonnement était simple : si la lumière se déplace à vitesse constante dans l'Ether, alors, si on fait une mesure de cette vitesse dans le sens du déplacement de la Terre par rapport à l'Ether, on doit obtenir un résultat plus faible que si la mesure est faite dans la direction opposée. La différence nous donne alors une estimation de la vitesse de la Terre dans l'Ether. |
Quel fût le résultat de l'expérience de Michelson-Morley ? Ils ne mesurèrent aucune différence ! La vitesse de la lumière est la même dans toutes les directions ! Impossible de mettre en évidence le mouvement de la Terre dans l'Ether!
Ce résultat, totalement contre-intuitif, fut à l'origine d'un débat scientifique fructueux entre les grands noms de la physique de l'époque : Lorentz, Voigt, Fitzgerald, Poincarè, et finalement Einstein.
En 1889, un court article fut publié par le physicien irlandais Fitzgerald dans la revue Science, dans lequel il explique que les résultats de l'expérience de Michelson-Morley peuvent être compris seulement si : " la longueur des objets matériels se modifie au cours de leur déplacement dans l'Ether, d'une quantité proportionnelle au carré du rapport de leur vitesse à celle de la lumière ".
En effet, l'expérience de Michelson-Morley fut répétée plusieurs fois, donnant systématiquement le même résultat, et on ne remettait plus en cause sa validité. La seule explication que l'on avait, et qui finalement sera la bonne, est que la taille des objets se modifie en fonction de leur déplacement et de leur vitesse dans l'espace !
L'unité de longueur et de temps doivent se modifier de sorte que lorsqu'on essai de mesurer la vitesse de la lumière dans toutes les directions et toutes les conditions (mais dans le vide), on obtient toujours le même résultat.
Poincaré saute le pas en 1905, dans un article où il se pose la question même de l'existence de l'Ether. Il écrit qu'un observateur ne possède en fait aucun moyen de dire s'il est en mouvement où au repos par rapport à un référentiel absolu, et que cette impossibilité doit être une loi générale de la nature.
Il faut donc maintenant reformuler les lois de changement de repère qui prennent en compte ces phénomènes de contraction spatiale et de dilatation du temps. C'est Lorentz qui le premier formule ces équations de changement de repère :
Soit un repère R2 qui se déplace par rapport à un repère R1 à la vitesse constante V sur l'axe des X, alors, les équations de changement de repère sont :
X2=(X1-V t1) / (1-V2/C2)1/2
Y2=Y1
Z2=Z1
t2=(t1-V X1/C2) / (1-V2/C2)1/2
Nous pouvons remarquer tout de suite que t2 est différent de t1 ! Les deux observateurs dans les référentiels R2 et R1 n'ont pas la même horloge !
On possédait maintenant grâce à Lorentz les équations de transformation, mais on n'en comprenait pas l'origine ! D'où peuvent bien venir de telles équations de changement de repère ? Comment les intégrer dans le reste de la physique ? Ce fut là le travail d'Einstein.
Le 30 Juin 1905, Einstein publie un papier dans lequel il pose toutes les bases de la théorie de la relativité restreinte (" special relativity " en anglais), qui est avant tout remarquable par une approche totalement novatrice du problème : Au lieu de présenter ses travaux comme une tentative d'expliquer un fait expérimental, il construit un nouveau principe qu'il justifie par sa beauté et sa simplicité. Dans l'introduction Einstein pose 2 postulats sur lesquels est basée toute la théorie :
Par ces deux postulats, Einstein retrouve les transformations de Lorentz, et montre qu'elle est totalement compatible avec les équations de Maxwell, résolvant enfin le paradoxe. La théorie de la relativité restreinte est n'est pas une théorie de la gravitation, c'est avant tout une théorie des changements de repères, mais elle ne concerne que les repères inertiels, c'est à dire ceux où quand un objet n'est soumis à aucune force, il se déplace selon en ligne droite.
Supposons qu'un observateur soit dans un référentiel R1, avec son unité de longueur et son horloge (unité de temps) et observe un corps au repos dans un référentiel inertiel R2, lui-même avec sa propre unité de longueur et son horloge.
Que verra notre observateur dans le référentiel 2
Contraction des longueurs
L'observateur 2, qui est en mouvement par rapport à l'objet verra la taille des objets se contracter dans le sens de son mouvement. Les directions perpendiculaires ne seront pas affectées. Supposons que l'objet soit une règle d'un mètre de longueur, 1 m mesuré dans le référentiel 1. Maintenant supposons que l'observateur dans le référentiel R2, en mouvement par rapport à R1, mesure cette règle. Il trouvera une taille en fait inférieure à un mètre, et égale à :
1 mètre / [ 1/(1-v2/C2)1/2 ]
où C est la vitesse de la lumière et v est la vitesse de déplacement de R2 par rapport à R1.
Il faut bien comprendre
que cette
contraction n'est pas une illusion ! La règle est
effectivement, et physiquement
plus courte quand on l'observe depuis le référentiel en
mouvement. Le facteur
1/(1-v2/C2)1/2 se retrouve partout en
relativité
restreinte. On l'appel le facteur Gamma, quand Gamma est très
proche de 1, on retrouve la
mécanique Newtonienne, par contre, plus V est grand, plus Gamma
est grand (divergence
vers +infini), et dans ce cas, la mécanique Newtonienne n'est
plus adaptée pour décrire
le mouvement des corps.
Dilatation du temps
L'effet de dilatation du temps est similaire à celui de la contraction des longueurs et s'énonce comme ceci : L'intervalle de temps entre deux événements, dans un référentiel dans lequel ces deux événements se font à des positions différentes (cas d'un repère en mouvement) est plus long que l'intervalle de temps dans le repère où les deux événements sont à la même position.
C'est une fois de plus surprenant. On peut l'illustrer comme ceci : supposons que dans notre référentiel 1, une horloge soit à dans une position fixe P, et émette toutes les secondes un rayon lumineux. Supposons qu'un observateur dans notre référentiel 2, en mouvement par rapport à 1, reçoive ces rayons lumineux et qu'il mesure l'intervalle de temps entre deux. Il mesurera un temps supérieur à une seconde !, Exactement : 1 seconde x gamma .
On peut énoncer ce principe encore autrement : une horloge en déplacement bat plus lentement qu'une horloge fixe.
Une fois de plus, ce n'est pas une illusion, cela a été vérifié expérimentalement. Par exemple en utilisant une horloge embarquée à bord d'un avion à réaction, on a pu mesurer qu'une fois l'avion retourné au sol, l'horloge présentait un léger retard par rapport à une horloge de référence, restée au sol.
Exemple: Cet effet est mesuré aussi couramment dans les accélérateurs de particules.
Voici un petit tableau donnant en fonction de la vitesse, le facteur gamma et la contraction des longueurs et la dilatation du temps qui en découlent :
| Vitesse (m/s) | Gamma | longueur (m) | temps (s) |
| 0 | 1 | 1 | 1 |
| 20 | 1.0000000000000022 | .9999999999999978 | 1+2.2 10-15 |
| 100 | 1.000000056 | 0.999999944 | 1.000000056 |
| 0.1C (30 106) | 1.005 | 0.995 | 1.005 |
| 0.9C | 2.29 | 0.44 | 2.29 |
| C | infini | 0 | 0 |
La relativité restreinte est une refonte totale de notre notion de l'espace et du temps : il n'existe ni de temps, ni d'espace absolu. La taille d'un objet et le temps entre deux événements dépend complètement du référentiel dans lequel on se place, et ne sont que des mesures locales. L'origine de cela est la constance de la vitesse de la lumière dans tous les repères. C'est LE principe qui est à l'origine de toute la relativité restreinte. En effet, la seule explication possible à ce phénomène est que les instruments de mesures, que les unités de temps et d'espace se déforment, pour que finalement la mesure de la vitesse de la lumière donne toujours le même résultat numérique (300000 km/s).
Cependant, il existe une grandeur qui pour tout corps se conserve, indépendamment du changement de repère. On appelle cela un invariant relativiste. Supposons qu'un corps, dans un référentiel inertiel se déplace de dx, dy, dz dans l'espace, et de dt dans le temps. Alors la grandeur :
L = dx2+dy2+dz2-Cdt2 est constante dans tous les repères. C'est une espèce de théorème de Pythagore généralisé à 4 dimensions Pour un photon, qui bien sûr se déplace exactement à la vitesse de la lumière, L=0. .
Le principe fondamental de la dynamique
Cette modification de la notion d'espace et du temps a des conséquences profondes également sur la dynamique, il faut reformuler le principe de la dynamique.
Celui que nous connaissons déjà, établit par Newton, est :
Somme des forces = Masse x Accélération
Or le terme d'accélération qui est le rapport d'une longueur sur un temps au carré, doit être également modifié et devient : Somme des forces = Gamma x Masse au repos x Accélération
On introduit également une notion de masse généralisée : si on redéfinit la notion de masse, en posant : masse = masse au repose x gamma, alors, on retrouve (de manière formelle) le principe de la dynamique de Newton.
Force= Masse x Accélération
où la Masse ici désigne (Masse au repos) x Gamma.
Un phénomène étonnant alors apparaît : la masse augmente avec la vitesse du corps, puisque gamma augmente. Quand V=0, gamma=1, la masse du corps est donc celle au repos, par contre, quand V augmente, gamma aussi, donc la masse fait de même (attention, ne confondons pas : la masse au repos du corps est la même, c'est la masse observée qui augmente !). Enfin, quand V tend vers C, le facteur gamma diverge vers + infini, et donc la masse également !
Maintenant, pourquoi ne peut-on pas aller plus vite que la vitesse de la lumière ? Une explication possible est que la masse d'un corps que l'on accélère diverge quand V tend vers C, ce qui implique que pour accélérer un corps à la vitesse de la lumière, selon le principe fondamental énoncé par Einstein, il faut lui appliquer une force infinie ! Ce qui est impossible.
Energie de masse
Dans sa théorie de la relativité restreinte, en plus de la dilatation du temps et de la contraction des longueurs, Einstein a mis en évidence une nouvelle forme d'énergie, que l'on appelle souvent "l'énergie au repos ", ou "énergie de mass e". Comme nous le savons, un corps en déplacement possède une certaine énergie cinétique. Mais Einstein montre qu'il en possède également une quand il est au repos, elle est donnée par la célèbre relation :
E= MC2
où M désigne la masse au repos.
Comment comprendre cette relation ? Elle montre que toute masse est équivalente à une énergie et inversement. Si on pouvait désintégrer un objet et le transformer en énergie pure, on obtiendrait une quantité d'énergie égale à MC2. C'est un nombre absolument énorme ! Elle est très utile en fusion nucléaire par exemple : quand on casse un noyau d'atome, la masse des constituants séparés du noyau est inférieure à celle du noyau lui-même. Cette différence de masse est convertie en énergie selon la relation E=MC2, c'est cette énergie que l'on récupère pour faire de l'électricité dans les centrales atomiques, ou plus tristement, dans les bombes nucléaires.
Enfin, l'énergie cinétique d'un corps n'est plus 0.5 MV2, mais : (gamma -1) x MC2.
Pour des vitesses faibles, on retombe bien sur le célèbre 0.5MV2. On voit donc que l'énergie totale d'un corps (énergie cinétique plus énergie de masse) est gamma MC2.
Pour V faible, l'énergie du corps est ~MC2, c'est à dire que son énergie cinétique est beaucoup plus faible que son énergie de masse, en général négligeable dans la vie de tous les jours. Par contre Quand V augmente, gamma augmente également, et l'énergie cinétique du corps devient comparable, voire beaucoup plus grande que son énergie de masse. C'est là un autre moyen de mesurer l'importance des effets relativistes sur un corps :
Quand son énergie de masse est beaucoup plus grande que son énergie cinétique, la physique de Newton est valable (en première approximation). Quand l'énergie cinétique est comparable, voire supérieure à l'énergie de masse, alors il faut utiliser la relativité restreinte.
En conclusion, la relativité restreinte détruit complètement la théorie de la mécanique construite par Newton : Elle transforme fondamentalement la notion d'espace et de temps, et reformule le principe de la dynamique.
Cependant, cette théorie est dite restreinte, c'est à dire qu'elle ne concerne que les repères inertiels. Elle ne peut pas traiter de la physique dans les repères accélérés.
C'est en voulant généraliser sa théorie à tous types de repères qu'Einstein invente la Relativité Générale, et plus qu'une théorie de la mécanique dans tous les repères, il y inclut complètement la gravitation et lui fait jouer un rôle central. Ainsi, la théorie de la relativité générale, comme nous allons le voir, est avant tout une théorie de la Gravitation.
La relativité générale
La naissance de la théorie de la relativité générale est une expérience quasi-personnelle pour Einstein. C'est en faisant une suite de raisonnements, et entre autres de nombreuses expériences de pensées et en ne se basant sur aucune expérimentation, qu'Einstein entre 1907 et 1916 mit au point la théorie de la relativité générale. Son ami, le mathématicien Grossman, l'initia à la théorie de la géométrie différentielle (Gauss, Rieman, etc..) qui paraissait alors un champ des mathématiques exotique, dont on ne soupçonnait pas alors les applications physiques.
Pour présenter cette théorie, nous ne suivrons pas le fil historique, car Einstein s'est de nombreuses fois trompé, puis corrigé, pour arriver finalement, en 1916 à la formulation correcte de la théorie, quasiment en même temps que le célèbre mathématicien Hilbert.
La théorie de la relativité générale est hautement mathématisée. Nous nous limiterons ici à des explications en essayant de ne pas trahir la signification des équations de la gravitation.
Le principe d'équivalence
Comment généraliser la théorie de la relativité restreinte à tous les types de repères ?
Le repère le plus simple qui ne soit pas inertiel 'est le repère uniformément accéléré, c'est à dire dont la vitesse (mesurée depuis un repère inertiel) augmente à un taux constant, du type V= A t, où A est l'accélération.
Voyons comment maintenant Einstein, par une expérience de pensée, montre comment relier cela à la notion de gravitation :
Considérons des personnes enfermées dans un ascenseur. Supposons que ce dernier est dans l'espace, attaché a un vaisseau spatial en accélération uniforme, par une corde. Que ressentent les personnes dans la cabine ? Elles sont attirées vers le sol de l'ascenseur, à cause de l'accélération constante de la cabine. Cette situation est tout à fait analogue à celle des objets à la surface de la Terre: nous sommes naturellement attirés vers le sol. Si ces personnes font des expériences de physique dans l'ascenseur (effets Doppler -lumineux- par exemple), ils pourront comprendre que l'ascenseur accélère à taux constant, mais ils ne sauront pas s'ils sont ou non dans un champ de gravitation ils pourront imaginer mille causes possibles de cette accélération constante, mais ne pourront décider laquelle est juste.
Cela peut s'écrire autrement : écrivons (bien qu'il soit approximatif) l'expression de l'accélération d'un corps de masse M dans un champ de gravitation crée par un corps de masse M', en physique newtonienne.
Mi A= G Mp M'/R2
On a noté Mi et Mp la masse inertielle et la masse pesante du corps de masse M (nous nous rappelons qu'expérimentalement Mp = M i= M ,
Pour que les observateurs dans l'ascenseur ne puissent pas décider s'ils sont ou non dans un champ de gravitation , il faut que l'accélération à laquelle ils sont soumis , soit indépendante de leur masse. Cependant, Le principe d'équivalence, s'il est vrai, IMPOSE que Mi=Mp, seul moyen pour que A ne dépende pas de M.
Ainsi, Einstein pose, comme un postulat de la relativité générale le principe d'équivalence, dont une conséquence est que Mi soit exactement égale à Mp. La remise en cause de ceci détruirait toute la théorie.
Retenons donc les deux choses suivantes :
Le principe d'équivalence : un champ de gravitation est localement équivalent à un repère soumis à une accélération uniforme. Ceci a pour conséquence l'égalité de la masse inertielle et de la masse pesante.
La Métrique de l'espace-temps
Le principe d'équivalence est la clef de la compréhension de la relativité générale et l'origine de l'approche complètement nouvelle de la gravitation. Il nous donne un moyen de décrire la gravitation autrement que par des forces, en utilisant directement la notion de repère uniformément accéléré.
Comment décrire un repère uniformément accéléré ? Quelles sont ses propriétés ? Nous nous contenterons ici de considérations générales. Premièrement, c'est un repère, où un corps soumis à aucune force ne suivra pas à priori des lignes droites, mais sera soumis à des forces dites inertielles, et suivra des courbes. L'exemple le plus simple (bien que ce soit un repère en accélération non uniforme), est le cas d'une bille qui roule sur un plateau tournant. Le plateau tournant est un référentiel accéléré, la bille, sur le plateau, ne suivra pas des lignes droites, mais des courbes à cause de la rotation du plateau. Bien que cet exemple ne soit pas exact, il permet de saisir l'essence de la description de la gravitation.
L'idée d'Einstein est de généraliser la notion de ligne droite, et la remplace par la notion de géodésique. Une géodésique est, dans un espace, le plus court chemin entre deux points. Dans un référentiel inertiel, le plus court chemin entre deux points de l'espace temps est une droite. On dit également que la métrique d'un référentiel inertiel est Euclidienne. Dans un espace euclidien, les géodésiques sont des droites.
Par contre, il existe des espaces où les géodésiques, le plus court chemin entre deux points, n'est plus une droite, mais une courbe. Par exemple, les espaces de Riemann, qui sont des sphères. Quel est à la surface d'une sphère, le plus court chemin entre deux points ? Par exemple, quel est le chemin que doit emprunter un avion pour aller de Paris à Los Angeles ?
L'idée la plus intuitive consiste à projeter une droite sur la surface de la sphère, qui va de Paris à L.A. C'est une GROSSE erreur. La droite est le plus court chemin entre deux points d'un plan, mais pas le plus court chemin entre deux points de la sphère. La géodésique sur la sphère est le cercle qui passe par les deux points et qui est centré sur le centre de cette sphère.
La trajectoire obtenue est une géodésique. Dans le cas du vol Paris - Los Angeles, cela explique pourquoi on monte si haut vers le Nord au cours du vol, on frôle même le cercle arctique.
| Une coccinelle , tantôt sur un plan, tantôt sur une sphère essaye de suivre des géodésiques (d'après Feynman) |
Cette notion de géodésique, dont on vient d'exposer ici un exemple à 2 dimensions (surface de la terre), se généralise tout à fait à 3, et 4 dimensions, mais dans ces cas là, il est très difficile de se représenter mentalement la forme de la géodésique. Cette derniére est donnée par un objet mathématique appelé le tenseur métrique. Ce tenseur métrique permet de calculer la distance, ds, entre deux points dans une espace quelconque. Dans le cas d'un espace inertiel à 4 dimensions (3 d'espace et une de temps), il donne :
ds2=dx2+dy2+dz2-Cdt2
On reconnaît là l'invariant relativiste décrit dans le cas de la relativité restreinte.
Einstein généralise le principe d'inertie de Galilée (un corps soumis à aucune force se déplace à vitesse constante en ligne droite), à tous les repères (accélérés ou non), et ne considère plus la gravitation comme une force, mais prend en compte son effet au travers d'un tenseur métrique. Dans ce cadre le principe d'inertie peut se reformuler ainsi : un corps plongé dans un champ de gravitation, s'il n'est soumis à aucune force, se déplacera le long d'une géodésique, celle-ci étant donnée par le tenseur de métrique. Dans le cas d'un champ de gravitation nul, où les géodésiques sont des droites, on retrouve bien le principe d'inertie de Galilée.
Einstein voit donc la gravitation comme une déformation géométrique de l'espace-temps. Les corps suivent des géodésiques à 4 dimensions (espace-temps).
Un corps, par sa masse, déforme et courbe l'espace autour de lui, et en change la forme et la métrique. John Weeler, physicien à l'université de Princeton disait : " La matière dit à l'espace-temps comment se courber, et l'espace courbé dit à la matière comment se déplacer "
Dans sa forme symbolique, le lien entre la matière et l'espace se fait par cette équation :
Gmn= 8 Pi x Tmn
où Gmn est le tenseur qui décrit la courbure de l'espace, et Tmn est le tenseur qui décrit le mouvement et la position des objets dans cet espace.
Comme pour la relativité restreinte, les effets de la relativité générale sont quasiment inexistants dans notre expérience de tous les jours. Pour mesurer son importance, on peut comparer le potentiel gravitationnel d'un corps, à son énergie de masse. On pose :
a =GM/RC2.
Quand a << 1 , les effets relativistes sont très faibles, c'est le cas de notre expérience de tous les jours. On ne sent pas les effets de déformation de l'espace. Quand a est entre 0.1 et 1, il faut absolument utiliser les équations d'Einstein.
Voici quelques ordres de grandeur :
Dans le système Solaire : a =10-9 pour la terre
a =10-6 à la surface du soleil
A la surface d'une étoile à neutron : a =0.1. Ainsi, le lieu privilégié de la relativité générale est celui où les corps sont très massifs, typiquement, c'est le champ d'investigation de la cosmologie.
Les équations d'Einstein sont rapidement extrêmement complexes, et de plus, le formalisme est d'une lourdeur qui est souvent rebutante. Elles ne sont résolues pour l'instant que pour des cas qui peuvent paraître très simples. Mais des approximations bien choisies permettent de décrire la plupart des phénomènes. Nous allons maintenant voir comment cette théorie a pu être validée par l'expérience (ce qui est rare), et quelques-unes de ses implications les plus surprenantes.
Tests de la relativité générale
La courbure du trajet de la lumière
L'une des prédictions les plus étonnante de la relativité générale est la courbure du trajet de la lumière lorsqu'elle passe au voisinage d'un corps massif. En effet, un corps comme le Soleil est suffisamment massif pour déformer l'espace autour de lui suffisamment pour que ce soit mesurable. Un rayon lumineux suivra une géodésique locale, qui ne sera plus une ligne droite. Ainsi, le rayon lumineux se verra dévié de sa trajectoire initiale.
Cet effet fut observé de manière convainquante lors de l'éclipse de 1919. Sir Arthur Eddington mesura la position des étoiles situées dans l'amas des Hyades (qui au moment de l'éclipse devait se trouver juste à coté du Soleil dans le ciel) avant et pendant l'éclipse. Eddington observa une modification de leur position apparente au moment de l'éclipse. Les rayons lumineux des étoiles, en passant au voisinage du Soleil ont bien été déviés de leur trajectoire initiale, en suivant la courbure de l'espace, en accord avec la théorie d'Einstein. C'est là le premier grand succès de la théorie de la relativité générale qui s'imposa rapidement dans les milieux scientifiques.
| Lettre d'Einstein à sa mère
lui annonçant la mise en évidence de la courbure de la
lumière par le Soleil. Pour ceux qui lisent l'allemand?.
|
La précession du périhélie de Mercure
Einstein a réussi à montrer que la précession inexpliquée de 42 secondes d'arc par siècle, est en fait due à la très légère déformation de l'espace induite par le Soleil. En relativité générale, les orbites des corps ne sont plus des courbes fermées, et, dans le cas de Mercure, la gravitation générale apporte une très faible correction aux équations de Newton, qui permet de retrouver exactement le taux de précession mesuré.
Décalage vers le rouge gravitationnel
Une autre conséquence prédite par Einstein est le décalage vers le rouge de la lumière quand elle est plongée dans un champ de gravitation. Attention ! Ce n'est pas exactement l'effet Doppler, bien que les effets soient semblables. Einstein montre qu'un rayon lumineux, quand il se propage dans un champ de gravitation, dépense une partie de son énergie pour "remonter " dans ce champ. Cette perte d'énergie ce manifeste alors par un décalage du spectre électromagnétique vers le rouge, et un affaiblissement du rayon lumineux. On peut l'interpréter également en utilisant le principe d'équivalence: le champ de gravitation dans lequel est plongé le photon est équivalent également à un repère uniformément accéléré qui s'éloigne de l'observateur, par conséquent, par effet Doppler, la longueur d'onde du photon augmente (décalage vers le rouge). Cela a été vérifié également expérimentalement.
Déformation du temps dans un champ de gravitation
Les équations d'Einstein montrent également qu'à l'instar d'un objet en mouvement dans le cadre de la relativité restreinte, un corps dans un champ de gravitation intense verra ses dimensions modifiées (augmentées) et son horloge ralentie. Cela également se mesure expérimentalement dans le champ de gravitation (faible) de la Terre.
Conséquences astrophysiques de la relativité générale
La topologie de l'univers
Comme nous l'avons dit, le champ d'application privilégié de la théorie de la relativité générale est la cosmologie, l'étude de l'origine de l'univers, et des structures à très grandes échelles. En effet, à ces distances, c'est la force de gravitation qui domine l'univers et lui donne sa structure. C'est ainsi que naturellement on peut se poser la question : Quelle est la forme de l'univers ? Que disent les équations d'Einstein ?
Einstein lui-même, s'étant posé ces question, vit tout d'abord que les équations prédisent naturellement un univers en expansion permanente : l'espace n'est pas stable et doit évoluer.
Il est connu que par convictions personnelles, Einstein (qui jusque là avait fait preuve d'une liberté de pensée sans pareille) ne put admettre un tel résultat. Il Introduisit alors dans ses équations, un terme appelé constante cosmologique (il avait mathématiquement droit de le faire) pour contrebalancer cet effet d'expansion.
Cependant, l'astronome Edwin Hubble découvrit en 1929 un mouvement d'éloignement global des galaxies, mettant par-là en évidence l'expansion de l'univers. Einstein reconnut plus tard qu'il avait fait une bien grande erreur en n'acceptant pas l'idée d'expansion de l'univers.
L'expansion d l'univers nous apparaît de la manière suivante: en regardant l'univers, on remarque qu'à grande échelle, les objets (galaxies) s'éloignent les uns des autres, et ce d'autant plus rapidement qu'ils sont éloignés. Cependant, cette vitesse d'expansion de l'univers est encore mal connue, elle se mesure par un paramètre appelé Ho, ou constant de Hubble , qui est la vitesse d'éloignement de deux objets en fonction de leur distance. On estime aujourd'hui qu'elle est environ de 70 km/s/Megaparsec ( une mégaparsec=3200 années lumiére).
| Relation entre la distance et la vitesse d'éloignement de quelques galaxies. Ce graphique a été obtenu par Hubble, et est à l'origine de la confirmation expérimentale de l'expansion de l'univers. L'axe des X est la distance en parsec (3.2 Années Lumière), en Y , ce sont des kilomètres par seconde. On remarque qu'il existe globalement une relation linéaire, ce qui signifie que la vitesse d'éloignement des objets est directement proportionnelle à leur distance. |
La relativité générale ne nous donne pas la forme de l'univers mais seulement sa métrique locale. En gros, on peut connaître la topologie mais pas la forme. Cependant, pour cette topologie les équations d'Einstein nous donnent deux directions possibles, en fonction de la densité de matière de l'univers :
Un espace ouvert, qui peut être infini, en expansion constante et indéfinie. Cet univers est condamné à devenir de plus en plus sombre et froid, de plus en plus vide, mais durera éternellement.
Un espace fermé, qui après un certain temps d'expansion entrera dans un régime de contraction, devenant de plus en plus chaud et lumineux, pour finalement disparaître dans une forme de big-bang inversé. Dans un espace fermé , un vaisseau en déplacement toujours dans la même direction revient à son point de départ en un temps fini.
Les ondes gravitationnelles
Une des conséquences les plus étonnantes de la relativité générale est la présence dans l'univers d'ondes gravitationnelles. En effet, une déformation de l'espace temps, induite par la présence d'un corps, ne disparaît pas comme ca. Elle se propage, à la vitesse de la lumière, comme une onde sonore ou lumineuse. Le soleil et les planètes engendrent des ondes gravitationnelles d'intensité beaucoup trop faible pour être détectée, cependant, des événements très violents, impliquant des corps très massifs dans l'univers peuvent causer des ondes d'intensité suffisante pour être détectées.
On n'a pas encore de preuve expérimentale directe de l'existence des ondes gravitationnelles. Cependant, les deux chercheurs Thylers et Hulse, astronomes américains, ont observé dans les années 70 la chute mutuelle en spirale, de deux pulsars (étoiles mortes, hyper-denses) ; Ils ont observé un ralentissement de leur vitesse de chute, compatibles avec une dissipation d'énergie sous forme d'ondes gravitationnelles. Cela leur a valu en 1993 le prix Nobel de Physique. Ces ondes devraient baigner tout l'univers, et leur détection nous donnerait accès à tout un pan d'informations encore totalement inconnu.
Le projet de détection est déjà avancé aux USA, avec le détecteur LIGO, au Caltech. un projet équivalent existe en Europe.
Les trous noirs
Comme nous les savons maintenant, la
lumière modifie son
parcourt au voisinage d'un fort champ de gravitation. Il peut cependant
parfois exister
des champs de gravitations tellement intenses , que la lumière elle
même chute
sur le coprs central et ne puisse plus s'en échapper. On appel
cela un trou-noir:
c'est un corps tellement dense que sa vitesse de libération
est supérieur à
celle de la lumière!! Ce qui est impossible comme on le sait. Un
objet qui tombe dans un
trou noir disparaît alors à jamais: il devient
complètement séparé de l'Univers
extérieur, car plus aucune information ne peut échapper
d'un trou noir. On décrit un
trou noir comme une sorte de puits sans fond de l'espace temps. Comment
se crée un
trou noir? Le scénario auquel on pense aujourd'hui est le
suivant : un étoile très
massive arrive à la fin de sa vie et explose en d'abord en
supernova. Puis , le c?ur de
l'étoile encore restant, commence à se contracter sous
l'action de son propre poids.
Cependant, ce poids est tellement énorme, que la force de
gravitation, responsable de
cette contraction, devient bien supérieure à toutes les
autres forces qui pourraient
contrebalancer cette contraction, celle ci se poursuit donc
indéfiniment. Par conséquent
la densité du c?ur ne cesse d'augmenter, dépasse
allègrement les 1000000000 tonnes/cm3.
Notre résidu d'étoile est désormais tellement
dense, que les forces de gravitation
qu'il exerce autour de lui sont fabuleuses! L'attraction
gravitationnelle qu'il exerce est
telle que même la lumière ne peut plus lui
échapper.
Autour du trou noir s'étend une frontière appelée Horizon, en dessous de laquelle la lumière ne peut plus s'échapper. Aucune information ne peut nous parvenir d'en dessous de cet Horizon. D'un point de vu physique, cette frontière correspond à une zone où le temps est gelé: vu de l'extérieur, le temps ne s'écoule plus à la surface du trou noir. C'est en quelque sorte la frontière entre notre univers, et l'espace intérieur du trou noir auquel nous ne pouvons avoir accès.
Quelle est la taille de cet horizon? On l'appel également Rayon de Schwarzschild . Pour le calculer, il suffit d'écrire que la vitesse de libération (calculée au chapitre 5) est plus grande que C. Il apparaît alors un rayon critique dont la valeur est :
R=2 GM/C2 (Rayon de Schwarzschild)
Où M est la masse de l'astre central , G la constante de la gravitation. Si la taille d'un corps est inférieure où égale à son rayon de Schwarzschild alors le corps est un trou noir. On appel le rapport du rayon de Schwarzschild sur le rayon réel , le paramètre gravitationnel. Il mesure en gros la compacité de l'objet, et est pour les objets courants, très inférieur à 1. S'il est proche de 1, le corps est presque un trou noir.
Quelques valeurs du paramètre
gravitationnel:
Atome : 10-43, Etre humain : 10-25, Terre : 10-9, Soleil: 10-6, Etoile à Neutron : 0,1, Univers (si fermé): ~1 (cette valeur est à considérer avec prudence, car elle dépend fortement des hypothèses faites sur la structure de l'univers, encore sujettes à caution.)
Que se passe-t-il dans un trou noir ? Nous ne le savons pas, car la matière y est tellement comprimée que nos connaissances physiques actuelles n'y sont pas applicables. Il est possible également qu'un trou noir soit une sorte de tunnel spatio-temporel vers un autre endroit , un autre temps de notre univers, ou d'un autre? C'est là une possibilité qui n'est pas à exclure, au sens où l'état actuel des théories ne l'exclue pas totalement. Cette possibilité a d'ailleurs inspiré de nombreux auteurs de science-fiction au passage, qui y voient un moyen de voyager dans l'univers, plus vite que la vitesse de la lumière. Mais cela reste encore complètement du domaine de l'imaginaire.
Le trou noir est un objet théorique
par excellence: la
théorie de la gravitation prévoie son existence de
manière naturelle. De plus, c'est
potentiellement une source d'énergie fabuleuse, qui peut
expliquer bien des phénomènes
observés dans l'univers. Sans qu'on ait pu formellement en
identifier un (un trou noir
est inobservable, le seule moyen d'en identifier est par la
déformation qu'il induit sur
son environnement), de nombreuses sources très
énergétiques peuvent être associées à
des trous noirs. Au sein de la communauté scientifique, leur
existence n'est pas remise
en question.
On soupçonne par exemple qu'il existe un trou noir au centre de la galaxie d'Andromède, au centre de la galaxie du Cygne, au c?ur de certaines sources intenses de rayons X.
En conclusion : La théorie de la relativité générale, à l'instar de sa grande soeur (la théorie Newtonienne), moins parfaite, est entrée dans la phase où les justifications expérimentales s'accumulent, et où à chaque fois, la théorie d'Einstein passe brillamment le test.
En dépit de ses grands succès, la relativité générale, présente un inconvénient majeur : elle est incompatible avec la mécanique quantique. Or, pour décrire les premiers instants de l'univers il faut absolument posséder une théorie unifiée de la gravitation et de la mécanique quantique, ce qui n'est fait encore qu'imparfaitement à l'heure actuelle. Les théories actuelles prévoient l'existence d'une particule, vecteur de l'interaction gravitationnelle, appelée le graviton qui pour l'instant ne peut pas être détectée dans les accélérateurs. L'avenir nous dira ce qu'il en est. Y aura-t-il une troisième théorie de la gravitation ?
La Relativité générale aujourdh'ui : Séminaire Poincarré - Thibault damour
 |
 |