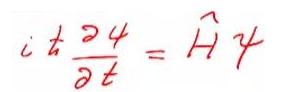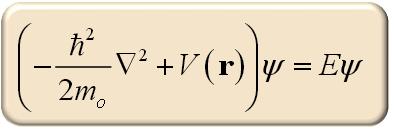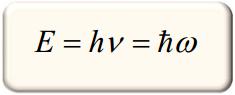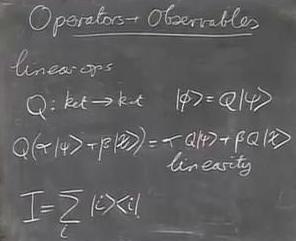Quelques
éléments sur la Mécanique Quantique |
Fonction
d'onde, amplitude
de probabilité, équation
de schrödinger, vecteur
d 'état de l'espace de Hilbert, ket,
bra, opérateurs,
opérateurs hermitiques, relation
de fermeture, orthonormalité
des vecteurs de base, propagateur,
valeurs
propres et vecteurs propres, observables,
la mécanique quantique utilise un niveau d'abstraction élevé
et un outillage mathématique de haut niveau dans lequel l'approche
probabiliste joue un rôle essentiel.
La mécanique quantique est la base de notre compréhension
des interactions fondamentales en physique et en chimie ( interactions
entre protons électrons et photons, états liées et
état libre des particules etc) à l'exception des phénomènes
liés à la gravitation.
Dans le domaine des particules relativistes ( qui vont à une vitesse
proche de celle de la lumière ) elle a été
élargie à la Théorie
Quantique des Champs.
Les concepts et les perceptions issus de la
mécanique quantique ne sont pas ceux du "sens commun".
La " manière d'agir " des particules élémentaires
d'écrite par la théorie semblent entraîner des paradoxes
quand on essaye de l' expliquer ou de la traduire en langage courant.
D'une certaine manière, on peut dire que la mécanique quantique
a modifié le sens du mot comprendre en ce qui concerne la physique
fondamentale.
Ce qui valide cette théorie est son extraordinaire pouvoir de
prédiction.
Depuis son origine jusqu' à nos jours ses prédictions expérimentalement
mesurables ont été vérifiées quotidiennement
dans des laboratoires du monde entier avec une précision inégalée
dans n'importe quel autre domaine.
Pour donner une idée du type de précision de la prédiction théorique, voici un exemple: (d'après Richard Feynman )
L'électron possède une grandeur
caractéristique le moment magnétique.
La valeur de cette grandeur peut être prédite et calculée
par la théorie quantique et elle peut aussi être mesurée
expérimentalement.
En comparant les deux chiffres nous avons:
Moment magnétique de l'électron théorique =
1, 001 159 652 140
Moment magnétique de l'électron mesuré
= 1, 001 159 652 193
(avec une incertitude de 10 sur les deux derniers chiffres pour la valeur
du moment magnétique mesuré, et une indétermination
de 27 sur les deux derniers chiffres du moment magnétique théorique
( due à l'indétermination sur la constante de couplage (j))
Cette précision est du même ordre de grandeur
que celle que l'on obtiendrait en mesurant la distance Los- Angeles -
New -York à l'épaisseur d'un cheveu près! (R.P.F.)
-------------------------------------------------------
Brève histoire de la mécanique quantique
1900 : Max Planck
Pour résoudre le spectre d'émission éléctromagnétique
d' un "corps noir",
Planck introduit la quantification de l'energie et la constante de Planck
h ) .
Les échanges d'énergie entre matière et rayonnement
sont quantifiés, ces échanges ne peuvent se faire de manière
continue mais doivent être proportionnel à hv ou h représente
la constante de Planck et v la fréquence du rayonnement.
1905 : Albert Einstein à partir de l'effet photo électrique repose l'aspect corpusculaire de la lumière.(quanta de lumière = photon d'énergie E = hv )
1913 : Niels Borh donne un premier modèle de l'atome d'hydrogène
1923- 1924 : Louis de Broglie généralise la dualité onde corpuscule et pose qu' à chaque particule doit être associée une onde avec E = hv )
1925 : Wolfgang Pauli : Principe d'exclusion de Pauli (deux fermions ne peuvent occuper le même état quantique)
1925 : Werner Heisenberg, Max Born, et Pascual Jordan formulent la description matricielle de la mécanique quantique.
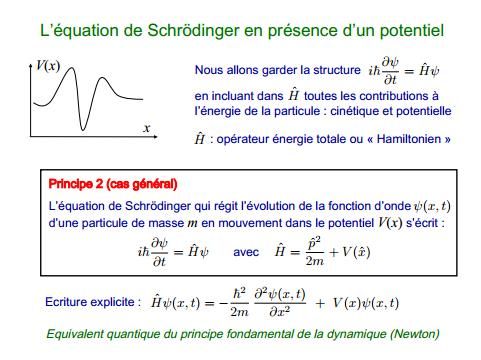
1926 : Erwin Schrödinger pose son équation de la fonction d'onde qui fonde la mécanique quantique ondulatoire
1927 : Max Born
montre que le carré du module de la fonction d'onde a la signification
d'une densité de probabilité de présence.
1927 : Paul Adrien Dirac
montre l'equivalence entre la mécanique quantique en représentation
de Schrödinger et en représentation d' Heisenberg .Il applique
aussi la fonction d'onde aux particules relativistes. ( équation
de Dirac)
1927 : Niels Borh, Werner Heisenberg et Max Born définissent l' Interprétation de Copenhague
1930 - 1945 Fermi et beaucoup d'autres : découverte puis utilisation de la radioactivite - fission - fusion
1948 : Richard Feynman résout les difficiles calculs de l'électrodynamique quantique en utilisant la forme lagrangienne de la MQ et son formalisme à base d'intégrale de chemin
1970 : Alain Aspect par son expérience sur le paradoxe E.P.R. confirme la non localité de la mécanique quantique.
Depuis Qubits, électrodynamique quantique en cavité, intrication quantique, décohérence,..
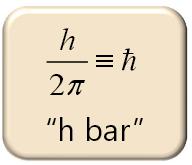
Quelques liens pour en savoir plus