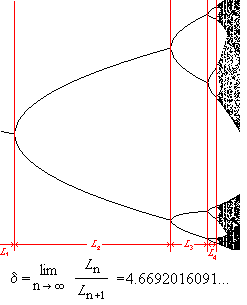

Bifurcations
Etonnament l'itération de nombreuses fonctions simples
répétées de nombreuses fois en prenant pour valeur
le résultat de l'itération précédente : x (
t+1) = f (x (t)) aboutit à des courbes
de bifurcation similaires
avec des constantes de bifurcation identiques
( Constantes de Feigenbaum )
Ces transitions appparaissent aussi dans de nombreux processus physiques, notemment ceux décrit par des équations différentielles non linéires. L' étude mathématique et physique de ces phénomènes se nomme la Théorie du Chaos.
Ci- dessous :
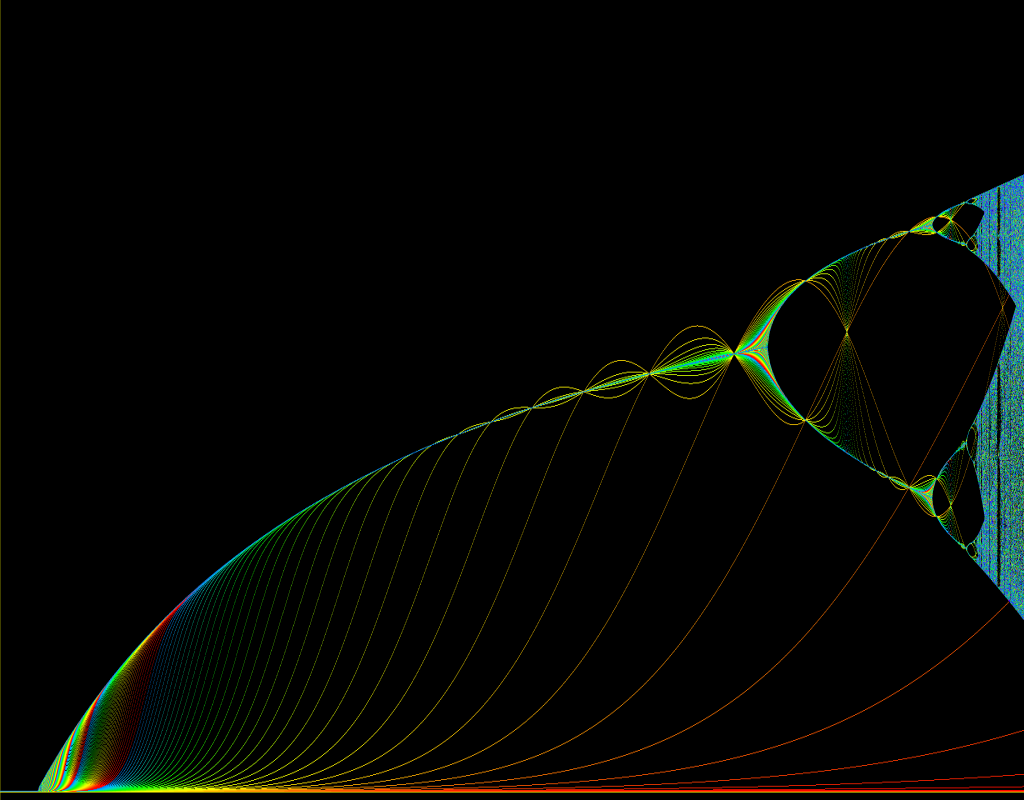
Diagramme de bifurcation obtenue après itérations de la fonction logistique
f ( n ) = a × n × ( 1 - n ).
"We applied the well known formula f ( n ) = a × n × (
1 - n ).
The formula was run 1500 times for each value of a from about 1.5 to 4.2
with n starting at 0.0001.
For those coming by about
the Feigenbaum's number, there are 5 x 60 digits after the decimal point:
4.
669201609102990671853203820466201617258185577475768632745651
343004134330211314737138689744023948013817165984855189815134
408627142027932522312442988890890859944935463236713411532481
714219947455644365823793202009561058330575458617652222070385
410646749494284981453391726200568755665952339875603825637225
Une courbe similaire avec des constantes identiques peut être obtenue avec par exemple la fonction x(t+1) = r sin x(t)
------------------
L' autosimilarité des structures, attracteurs et attracteurs étranges