Les deux textes ci-dessous proviennent de commentaires de Sébastien Fromenteau, allias Cosmo_seb, emminent cosmologiste théoricien, ils ont été écrit lors de discussions sur le forum d' un FLOT publié sur FUN

Gravité! Du Big-Bang aux Trous Noirs

organisé en avril et mai 2015 par l' A.P.C. (AstroParticule et Comologie ) sous la direction de M. Pierre Binétruy et par l' Université Paris Diderot

publié avec l'accord de l'auteur (Cosmo_seb)

Je suis donc pris au piège! Là ça va être bien plus technique. Je vais essayer d'expliquer ça aussi simplement que possible.

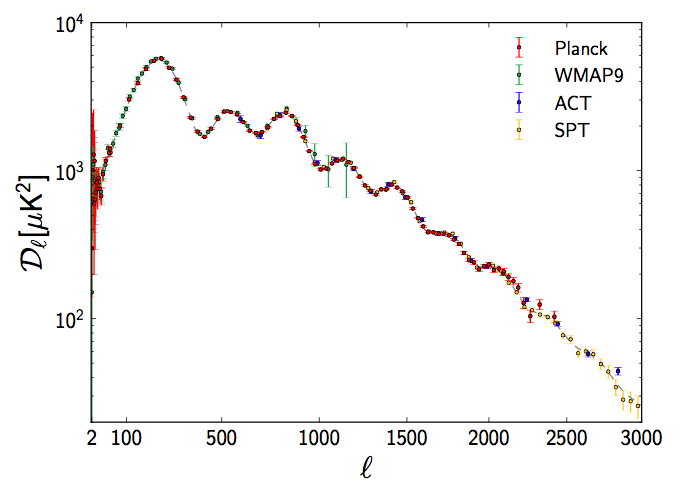La courbe représente la corrélation de température (en micro-Kelvin au carré µK2) en fonction de la taille regardé sur le ciel l.

En clair, on regarde s'il y a une corrélation de température en fonction de chaque taille. Plus l est grand et plus l'échelle regardé est petite car il s'agit de l'espace de Fourier.

S'il n'y a pas de processus qu'il fait que des perturbations d'une même taille donné soit toutes avec la même température alors la valeur de la corrélation tombe à 0. Le fait que cette courbe soit non nulle montre qu'il y a un processus qui donne une température particulière au zones (perturbations) d'une taille donnée.

Cette température correspond à l'état d'oscillation des perturbations. Si elles sont en étant de compression elles sont plus chaudes et si elles sont en dilatation elles sont plus froides.

Il faut donc que les perturbations d'une même taille donnée soient dans le même état d'oscillation. Ceci est rendu possible grâce à la période d'inflation. Les perturbations sont toutes crées dans leur état initial et commencent à comprimer en même temps et selon la même physique. Donc 2 perturbations d'une même taille vont comprimer puis se dilater se lin même processus et pendant le même temps (380 000 ans). Elles vont donc être dans le même état d'oscillation au moment de l'émission du CMB. C'est un mécanisme essentiel.

L'information qu'on mesure est le produit de l'écart à la moyenne Deleta T× Delta T des températures. En clair:
si les perturbations d'une taille l donné sont en phase d'oscillation intermédiaire, leur écart à la température moyenne est faible (Delta T~0). On obtient donc une valeur de corrélation (qui retire la moyenne) faible.
si les perturbations d'une taille l donné sont en phase de compression, leur température est plus grande que la moyenne (Delta T>0). On trouve donc une valeur de corrélation grande (Delta T)2
si les perturbations d'une taille l donné sont en phase de dilatation, leur température est plus faible que la moyenne. On trouve donc une valeur de corrélation grande car il s'agit du produit de l'écart (DeltaT<0). Donc (DeltaT)2 est grand aussi.

Quand on part de la gauche, on regarde les très grandes perturbations qui n'ont pas eu le temps de se compresser beaucoup car trop grandes pour le faire en 380000 ans.

On commence à se déplacer avers la droite. On voit que la courbe augmente car on regarde des perturbations de plus en plus petite jusqu'à arriver sur le pic qui correspond aux perturbations de la taille qui ont exactement eu le temps de compresser complètement. C'est le premier pic.

On continu à se déplacer vers la droite. On voit que la corrélation diminue. Car les perturbations sont plus petites. Elles ont eu les temps de compresser + commencer à dilater. On descend jusqu'au creux. Il correspond aux perturbations qui ont eu le temps de comprimer et de dilater jusqu'à se retrouver dans leur état initial.

On continue vers la droite. La corrélation remonte car les perturbations sont encore plus petite et ont eu le temps de comprimer + dilater au delà de leur état initial. Elles sont donc plus froide que la moyenne. En continuant on trouve le second pic qui correspond aux perturbations qui sont dans l'état de dilatation maximal. Elles ont la taille qui permet d'avoir fait une compression + une dilatation complète.

Le 3èmé pic correspond à à la deuxième compression maximale => 1comp + 1dilat + 1comp

Le 4èmé pic correspond à à la deuxième dilatation maximale => 1comp + 1dilat + 1comp + 1dilat

Et ainsi de suite.

Rapport entre 2eme et 3eme pic

Plus une perturbation est grande, plus elle est massive et donc plus l'écart Delta T de température peut être grand. De plus, le processus que nous considérons n'est pas parfait. Il y a dissipation d'énergie et donc l'oscillation ne peut pas se faire 100 fois. Il y a amortissement (Silk Damping). On attend donc que les toutes petites perturbations est arrêté d'oscillé et donc se retrouve toutes avec la température moyenne et donc une corrélation nulle. On attend donc une régression progressive de la corrélation quand l augmente. Il faut imaginer une pente constante autour de laquelle on dessine une sinusoïdale.

Lorsqu'on dessine cela, on n'attend que le 3eme pic soit en dessous du 2ème. Sauf si la compression permet de faire un Delta T plus important que la dilatation. Dans ce cas les pics liés à la compression ont plus d'amplitude que ceux de la dilatation. Or ceci n'est pas possible sans introduire quelque chose d'autre que l'oscillation de la matière avec les photons.

La matière noire permet ceci. En effet, comme elle n'interagit pas avec les photon, elle ne subit pas la dilatation. Ainsi, elle reste bien sagement au centre. Ainsi, le potentiel gravitationnel central reste assez conséquent et rattrape plus vite la phase de dilatation l'empêchant d'aller trop loin. A contrario, ce potentiel renforce la phase de compression. Donc On attend bien a observer des pics impairs (compression) plus important que les pairs (dilatation) avec de la matière noire. On ne peut pas expliquer cette asymétrie en modifiant la seconde loi de Newton (MOND)
Plus

posté par Cosmo_seb Équipe pédagogique

je ne suis pas tout à fait d'accord. Je pense avoir répondu à la question que j'ai compris. J'ai compris qu'il y avait un soucis entre homogénéisation et échange d'information et je pense avoir répondu à cette question.

Quand vous me dites que pour autant, l'inflation n'explique pas pourquoi la zone initiale était homogène je vous répond que vous avez raison, qu'il s'agit d'un postulat.

Maintenant je suis d'accord avec vous pour dire que la grande question sous-jacente est de comprendre pourquoi l'inflation est nécessaire à la reproduction des observations du CMB.

Le point principal est dans l'observation des anisotropies du CMB. Nous avons déjà évoqué qu'il s'agissait d'un "cloud in cloud problem". Il y a des perturbations dans des perturbations plus grandes dans des perturbations plus grandes....etc

Deux grandes questions s'imposent:

Comment expliquer l'existence de ces perturbations à toutes les échelles
plus précisément comment expliquer les perturbations non-causales observées par COBE en 1992
Comment expliquer la corrélation de l'état d'oscillation (compression/dilatation) des perturbations au moment du CMB
Expliquer l'apparente platitude de l'Univers observable

Juste pour rappel, la théorie de l'inflation date de 1981, donc les observations mentionnées n'existaient pas encore. C'est très important, car ces observations seront alors des test des prédictions de la théorie de l'inflation.

Comme je l'avais expliqué dans un FLOT précédent, la théorie de l'inflation permet de créer les perturbations par les fluctuations quantiques. Elles sont produites durant la phase d'expansion et ce durant toute la phase d'expansion. Ainsi, les perturbations générées au début sont devenues plus grandes que l'univers observable et les plus petites ont été générées à la fin de la phase d'inflation. Selon ce mécanisme il est possible de prédire les propriétés statistiques des perturbations => son spectre de puissance. Ainsi, le spectre de puissance était prédit avant l'observation des perturbations et il est en accord avec elles.

Le fait d'observer le spectre de puissance de température du CMB non nul veut dire que les perturbations d'une taille donnée ont la même température. Autrement dit, elles doivent se trouver dans le même état de compression dilatation. J'ai fait la présentation détaillée de ce mécanisme ici. Pour obtenir cette corrélation dans l'état d'oscillation des perturbations, il faut qu'elles se trouvent dans le même état initial au même moment (instant B de votre explication). En clair, il faut avoir créé toutes les perturbations d'une taille donnée au même instant. Encore plus fort, la prédiction/observation de l'état d'oscillation en fonction de la taille n'est compatible qu'avec le fait que toutes les perturbations ont commencé à évoluer (osciller) au même instant. Honnêtement je ne connais aucune autre théorie qui permette ces conditions initiales si particulières.

Comme expliqué dans le FLOT que j'ai mis en lien précédemment, le premier pic correspond aux perturbations qui ont exactement la taille de l'horizon causal au moment du CMB. Les points qui sont plus à gauche que ce pic, sur la figure du spectre de puissance de température, montrent qu'il y a des perturbations plus grandes que l'horizon causal. Ces perturbations étaient prédites par l'inflation et ont été vécu comme une évidence incroyable de cette théorie quand COBE les a observé.

Donc j'espère que vous comprenez mieux en quoi les conditions initiales à l'instant B sont complexes et que l'inflation permet de les avoir. Et que le fait qu'on parte d'un postulat que la zone nécessaire avant inflation était homogène est un coût finalement acceptable à la vue de tout ce qu'apporte l'inflation.

posté par Cosmo_seb Équipe pédagogique

J'en profite tout de même pour ajouter un point, il n'est pas nécessaire que l'ensemble de l'Univers soit homogène. Il est nécessaire qu'au moins l'univers observable le soit. C'est pour cette raison qu'il n'y a pas nécessité que l'infini de départ soit homogène mais seulement une zone réduite qui englobe ce qu'est devenu l'univers observable.

-------------------------------

..