L' ensemble de Mandelbrot, les fractales et la théorie du chaos

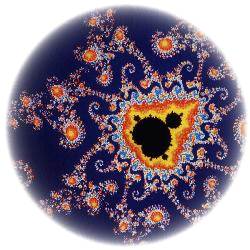
La figure ci-dessous est une représentation de l' ensemble de Mandelbrot

Un nombre complexe c appartient à l' ensemble de Mandelbrot si et seulement si la suite Z(0) = 0, Z(n+1) = Z(n) x Z(n) + c ne diverge pas à l'infini.

Dans l'image ci-dessus, représentant le plan complexe, les points appartenants à l'ensemble sont coloriés en noir.
La couleur des autres points dépend de la vitesse à laquelle cette suite diverge vers l'infini pour cette valeur du nombre complexe.

Une des particularités de cet ensemble est l'extrème complexité des ses frontières :
C'est un objet fractal. ( terme inventé par Benoit Mandelbrot )

Une autre particularité des ensembles fractals est l'autosimilarité des structures.
Si on zoom sur un ensemble fractals, quelque soit l'échelle, les mêmes formes réapparaissent sans que l'ensemble soit jamais srtictement identique.

Voir l'ensemble de Mandelbrot de manière dynamique en zommant dessus => http://www.syti.net/Fractals.html

Note : l' ensemble de Mandelbrot permet aussi d'indicer les ensembles de Julia qui sont eux aussi des ensembles fractals

Adrien Douady et John Hubard en 1985 démontre que l'ensemble de Mandelbrot est localement connexe.